Wofür steht eigentlich „SIX SIGMA“?
Erstelldatum: 04. Okt. 2017 | zuletzt aktualisiert: 10. Okt. 2021 | Dr. Urte Helling | 2 min. | PDF-Version
SIX SIGMA – bei einer DER Top-10 Qualitäts- und Managementmethoden weltweit, ist der Name Programm. Wer sich ein wenig an Mathematik und Statistik zurückerinnert, der ahnt bereits, dass bei der Optimierung von Prozessen die Standardnormalverteilung eine wichtige Rolle spielt und damit die Kenngröße der „Standardabweichung“ – und schon sind wir beim Sigma (σ). Schauen wir nachfolgend genauer hin …
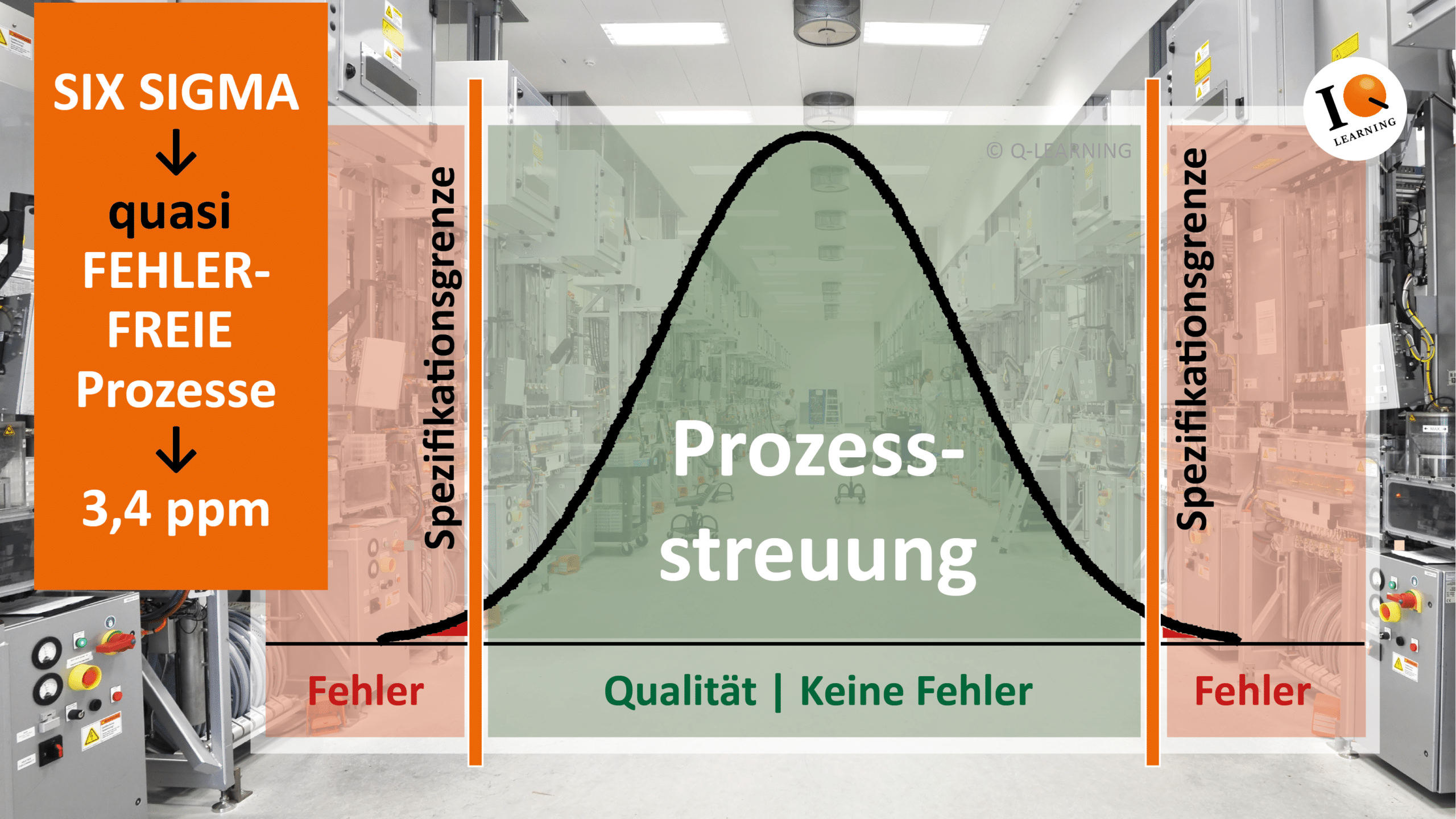
Der Begriff SIX SIGMA ist Synonym für (quasi) fehlerfreie Prozesse: Lediglich 3,4 ppm Fehleranteile (Ergebnisse außerhalb der Spezifikationsvorgaben) sind zu verzeichnen.
Fehlerfreiheit als Maxime
Ziel von Six Sigma sind nahezu fehlerfreie Abläufe, Produkte und Prozesse. Diese setzen ein hohes Maß an Prozessgüte voraus. Prozessgüte umschreibt die Fähigkeit eines Prozesses, das von ihm verlangte Produkt (bzw. die Dienstleistung, den Vorgang, die Konstruktion etc.) ohne Abweichung immer und immer wieder zu reproduzieren. Je höher das Maß der Prozessgüte, desto geringer ist die Wahrscheinlichkeit von Abweichung, desto geringer ist das Auftreten von Fehlern.
Streuung ist der größte Feind
Im Rahmen der prozessualen Reproduktion kommt es in der Praxis jedoch zu ungewollten Abweichungen. Prozesse variieren – wenn auch nur in kleinsten Nuancen – um ihre Vorgabewerte. Es kommt zu Streuung in den Werten, der sogenannten Prozessstreuung. Gehen wir davon aus, dass es sich um einen grundsätzlich nicht von außen gestörten Prozess handelt, dann unterliegt der Prozess ausschließlich einem gewissen Grundrauschen und damit minimalen Abweichungen.
Erinnern Sie sich an die Normalverteilung?
Das Grundrauschen lässt sich mathematisch-statistisch durch die Gauß’sche Normalverteilung abbilden, die nicht nur in der Schule, sondern ggf. auch einmal auf einem 10 DM Schein Ihr Leben kreuzte. Diese in der Statistik so wichtige Verteilungsform, auch als Glockenkurve bezeichnet, wird durch zwei Parameter beschrieben: Den Mittelwert μ, der die Lage der Kurve definiert, und die Standardabweichung σ, die die Breite der Kurve definiert und damit die Streuung des Prozesses beschreibt.
Die Standardnormalverteilung ist auch bekannt als die Gaußsche Glockenkurve. Sie ist charakterisiert durch ihre beiden Kennwerte, den Mittelwert μ und die Streuung σ.
Je schlanker, desto besser
Ein normalverteilter Prozess verläuft gewöhnlich nicht im luftleeren Raum, sondern hat sich gewissen Anforderungen zu unterwerfen. Diese sog. Spezifikationen bringen Ober- und Untergrenzen mit sich, an denen sich die Spreu vom Weizen trennt: Alle Prozessergebnisse innerhalb der Spezifikationsgrenzen sind gut, alle außerhalb liegenden Prozessergebnisse fehlerhaft und schlecht, da sie die Vorgaben nicht erfüllten. Sie müssen nachgearbeitet, weggeworfen werden oder führen später ggf. zu Problemen funktionaler und auch monetärer Art. Der Prozess muss also seine Grenzen klar im Auge behalten und hat somit ein klares Schönheitsideal: Je schlanker, desto besser – oder: So schlank wie nötig.
Sechs Sigma: 99,99966 % Qualität
Aber wie schlank soll er nun sein der Prozess, damit er als „gut“ bezeichnet werden kann? SIX SIGMA hat hier eine klare Vorstellung: Sechs Standardabweichungen links und sechs rechts des Mittelwerts müssen innerhalb der Spezifikationsvorgaben liegen. Dann spricht man von einem „SIX SIGMA Prozess“, der auf Basis der Normalverteilung 99,99966 % Qualität hervorbringt und nur 3,4 ppm Ereignisse als fehlerhaft zu bemängeln lässt (3,4 Fehleranteile pro 1.000.000 Einheiten). Ein Ergebnis, dass für die meisten Industriezweige wirtschaftlich sehr erstrebenswert ist, da es die sonst massiven Fehlerkosten attraktiv zu minimieren vermag.
Merke: Six Sigma und das Sigma-Niveau
- Das Sigma-Niveau eines Prozesses beschreibt die Prozessgüte.
- Je größer der Sigma-Wert ist, desto höher ist auch die Prozessgüte.
- Das Ziel von SIX SIGMA (6σ) umschreibt eine Fehlerwahrscheinlichkeit von 3,4 ppm bzw. eine Qualität von 99,99966 % – nahezu fehlerfrei.
Dr. Urte Helling
SIX SIGMA Master Black Belt
Dr. Urte Helling ist Gründerin von Q-LEARNING. Aus der Automobilindustrie kommend und auf zahlreiche Methodenausbildungen blickend widmet sie sich seit über zehn Jahren der Vermittlung, Anwendung und Weiterentwicklung von Qualitätsmethoden.
© Q-LEARNING | QLMB-4503